Research

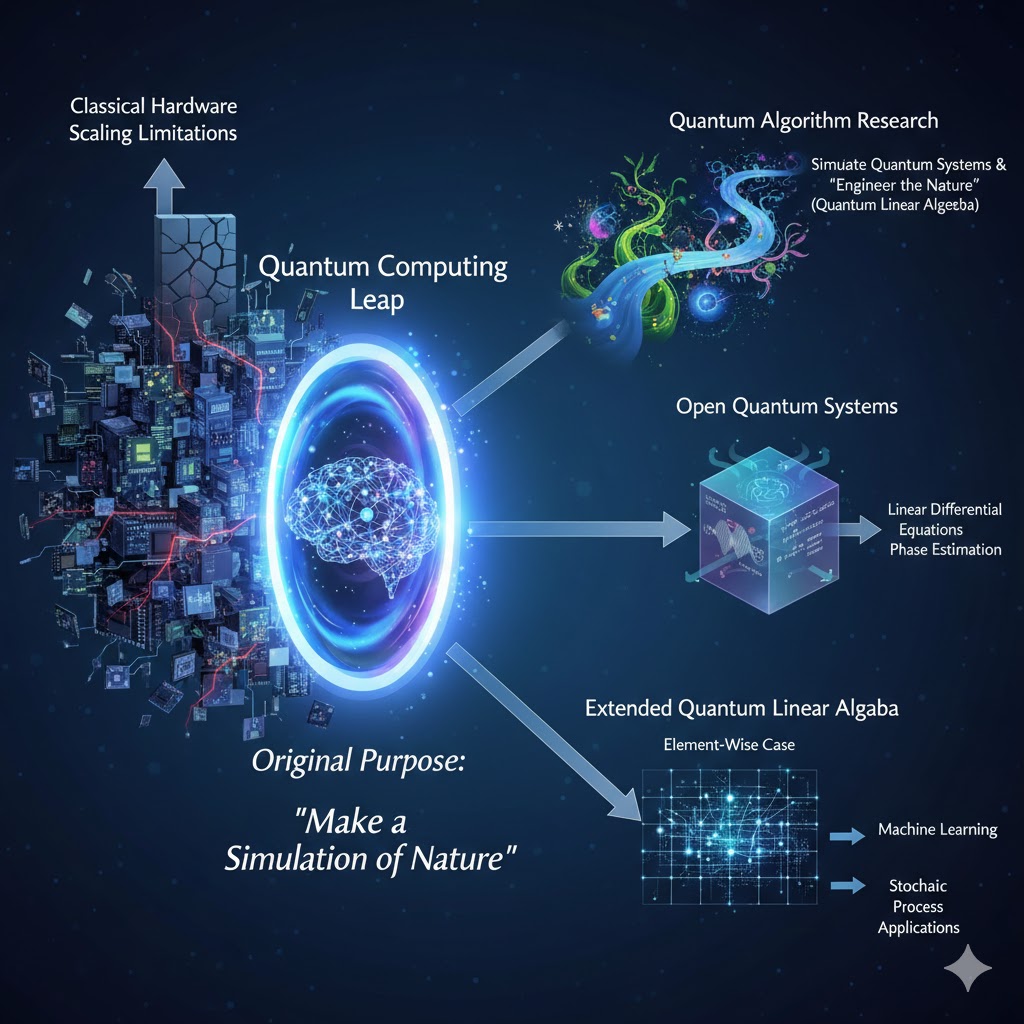
The development of quantum computing provides the next leap in computational capability, which is crucial since we are approaching the limitations of classical hardware scaling. As the original purpose of quantum computing is to “make a simulation of Nature”, quantum algorithm research focuses on how to simulate the quantum systems, and “engineer the nature” for applications. People also call this engineering the quantum linear algebra. Our works have explored the power of open quantum system for linear differential equations and deep relation with phase estimation. Also, we have extended quantum linear algebra to the element-wise case and applied it for machine learning, and stochastic process applications.

Selected works:

• Z. Shang, N. Guo, P. Rebentrost, A. Aspuru-Guzik, T. Li, Q. Zhao, Fast-forwardable Lindbladians imply quantum phase estimation, QIP 2026
• N. Guo, etc., Quantum linear algebra is all you need for Transformer architectures, arXiv:2402.16714
• N. Guo, K. Mitarai, K. Fujii, Nonlinear transformation of complex amplitudes via quantum singular value transformation, Phys. Rev. Research (2024)
• Z. Shang, N Guo, D An, Q Zhao, Design nearly optimal quantum algorithm for linear differential equations via Lindbladians, Physical Review Letters (2025)

As we confront the immense complexity and environmental sensitivity of near-term quantum processors, the field of AI for Quantum provides a critical pathway toward practical quantum advantage. This discipline leverages powerful classical machine learning methods to address fundamental challenges in building and operating quantum computers. This also includes the theoretical analysis of the learnability of quantum states and the training of machine learning models for quantum systems.

Selected works:

• L. Ming, N. Guo, M. Luo, P. Rebentrost, Provable learning of quantum states with graphical models, arXiv:2309.09235